Project 2
cs599 Parallel Programming and Algorithms
20 Points
Due Mar. 16, 2015 at Midnight
You must run your program on Stampede to receive full points for this assignment
Instructions for running your program on Stampede are provided at the end of this document

Description

Objective:  To learn about MPI collective operations, random numbers, structures, pointers, and using multiple source files in C.

A Simple Genetic Algorithm

Genetic algorithms make use of ideas from population genetics and molecular genetics to solve a problem.  These concepts are "survival of the fittest", mating, crossover, and mutation, to name a few. Typically in a population, parents from a population give rise to children, some of which are more fit than others.  Individuals that are fit tend to survive longer than those who are unfit; obviously, this is known a survival of the fittest.  When a child is produced, the genetic material of the parents is intermingled to form a child.  This mixing of genetic material is called crossover.  Moreover, sometimes when a child is formed, the child's genetic material changes at random due to environmental factors.  This type of random change is known as mutation.  Populations go through a cycle of mating, creating children, children becoming parents, and eventual parent death known as a generation.

Computer scientists eventually used the concepts listed above to create optimization algorithms.  Such algorithms have been called genetic or evolutionary algorithms because they use a "population" of values chosen at random to find the optimal solution to a function (or a set of functions).  These populations typically contain a set of parents and children.  Parents from these populations of values "mate" (that is, their values are combined or "crossed over" somehow) to form children.  After these children have been formed, their values are "mutated" (i.e. slightly modified) at random.  Thereafter, children whose function values are good (e.g. smaller for a function that is to be minimized) are kept and replace parents whose function values are bad (e.g. larger for a function that is to be minimized).  This process simulates "survival of the fittest."  This process is repeated a number of times so that a good population can be formed.  The number of times this process is to be repeated is also known as the number of generations.

Specification:

For project 2, you are to write an MPI program that will find the minimum of a two-dimensional function (e.g. y = x² ) bounded within a certain area (e.g. -5.0 < x < 5.0).  To accomplish this task, you must first generate a number of solutions at random within the bounds of the problem (e.g. 50 solutions).  Note that each process should generate an equal number of solutions. For example, if there are to be 50 total solutions and there are five processes, each process should generate 10 solutions. Thereafter, you are to use pairs of these solutions, called "parents", to produce a number of new solutions (e.g. 10 new solutions), called "children".  A description of how to choose parents is provided in the description of the functions below.  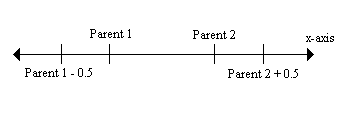These "children" must be chosen by picking a value at random between the x value of the first parent minus 0.5*alpha and the x value of the second parent plus 0.5*alpha as shown in the image below assuming that the first parent has the smaller x value, and then evaluating the function (e.g. y = x² ) at the new x value.  Note that a child should not fall outside of the bounds for the problem.  If it does, you must clamp the result such that it falls within the correct interval.  Note that in the image below, alpha is set to 1.0. You must provide a value for alpha in your program as a constant that is no more than 1/100 of the range of the x values.



After creating the desired number of children (10 in this case), these children are compared against the worst of the parents.  If the y value of a child is better than one of the worst of the parents in one process, the child becomes a parent; otherwise, the child is discarded.  Thus, those children that are better than the worst of the parents are added to the population to replace the worst parents.  This process should repeat itself for the number of times or "generations" that the user has requested.  An outline of the program and example output for a serial version of the program follows.

Program Outline:

The source code for project 2 should be placed in files named ga.h, ga.c, and prog2.c,   Do NOT give the files different names.  You will lose points if you give the file any other names than those provided above. 

ga.h

In ga.h, you should provide function prototypes, a definition of the struct that you will use, and declarations for any constants that you will use in your program.  Important: you do not yet know how to transfer structures with MPI. This means that you will need to move your data out of a structure before you transfer from one process to another.  You should have at least the following four function prototypes in your header file:

void initialize_population(individual []);
void make_children(individual [], individual []);
void evaluate_expression(double, double *);
void cull_individuals(individual [], individual []);

You may use other functions to aid yourself in making each of the above functions more manageable; however, additional functions are not required.  Any additional functions MUST be put in the same files (i.e. ga.h, ga.c, prog2.c).

ga.c

In ga.c, you must provide definitions for the functions above.  The initialize_population function must take the array of parents that the current process will use as a parameter and initialize each of the parent x values to a random value between XMIN (the minimum x value) and XMAX (the maximum x value).  Note that a random value between XMIN and XMAX can be chosen using the following formula:

(XMAX - XMIN) * ( (double) rand() / (double) RAND_MAX) + XMIN

Note that RAND_MAX is the maximum random value used by the C programming language and is available by using #include <stdlib.h>.  After initializing the x values for the parents, you must call the evaluate_expression function (which must evaluate an expression such as y = x²) on each of the given parents to set the y values for each of the parents.

Note that it is highly recommended that you use a different pseudorandom number generator to generate values. The Mersenne Twister is an excellent pseudorandom number generator and has a period of 2^19937. You can find example code that makes use of this pseudorandom number generator at the following link. The make_children function must take the parent and child arrays as parameters and choose the children from the parents using crossover and mutation.  To create a child, choose two parents at random from the array of parents, and ensure that the two parents are not from the same process. In each process, you should choose one parent from that process and one from a neighboring process. You should use a different neighbor in each iteration (e.g. in the first iteration choose the neighbor at rank+1 and in the next choose the neighbor with rank-1, and repeat).  Next, perform crossover.  This means that you will use the two parents to create one child.  In this case, children must be chosen by picking a value at random between the x value of the first parent minus 0.5*alpha and the x value of the second parent plus 0.5*alpha as shown in the image below assuming that the first parent has the smaller x value, and then evaluating the function (y = x² ) at the new x value.



Use the following formula to perform the crossover:

children[i].x = ( (parents[rv1].x+.5*alpha) - (parents[rv2].x-.5*alpha) )* ( (double) rand()/(double) RAND_MAX ) + (parents[rv2].x-.5*alpha);

Note that the formula above assumes that rv1 is the index of the larger parent.  You should ensure that this is true in your program.

After you have performed crossover on a child, you must then perform mutation on that child.  This will ensure that there is some variation within the set of children and will help to move a child out of a local minimum if one does exist.  The mutation operation in this program should add a random number between -0.1*beta and 0.1*beta to the child.  Ensure that beta is a value that is less than 1/1000 of the range in x. Mutation can be performed using the following formula:

children[i].x = children[i].x + .2*beta*(rand()/(double)RAND_MAX-.5);

Note that a child should not fall outside of the bounds for the problem.  If it does, you must clamp (change) the result so that it lies within the bounds for the problem.

Once the x value for the child has been produced using crossover and mutation, use the evaluate_expression function to set the y value for the child.

The process described above should be repeated for each child in each process.

Finally, for the cull_individuals function, you must attempt to add children to the array of parents.  Since the array of parents has a fixed size, you must remove or cull parents from this array before new children may become parents.  To do this, you must select the set of parents that are worse than the children.  Note that we are assuming that the number of children is smaller than the number of parents.  You may do this by locally searching for the worst parents within each process, marking their positions using an additional array, and by sorting the local list of children from highest y value to lowest y value.  Then add children to the array of parents by comparing them to the worst parents.  Most of the code for this function is as follows below.

int dead_parents[NC] = {-1};
int sorted_children[NC];
int i, j, maxval;

for( i = 0; i < NC; i++)
    sorted_children[i] = i;

for( i = 0; i < NC-1; i++)
    for( j = i + 1; j < NC; j++)
        if ( children[sorted_children[i]].y < children[sorted_children[j]].y )
            /* swap sorted_children[i] and sorted_children[j] here */

for(i = 0; i < NC; i++)
{
    maxval = 0;

    while(i > 0 && parents[maxval].y > parents[dead_parents[i-1]].y)
        maxval++;

    for(j = 0; j < NP; j++)
    {
        if(i > 0)
        {
            if(parents[j].y < parents[dead_parents[i-1]].y && parents[j].y > parents[maxval].y)
           
                maxval = j;
        }
        else
        {
            if(parents[j].y > parents[maxval].y)
                maxval = j;
        }
    }
    dead_parents[i] = maxval;
}

for(i = 0, j = 0; i < NC; i++)
{
    if(children[sorted_children[i]].y < parents[deadparents[j]].y)
    {
        parents[dead_parents[j]].y = children[sorted_children[i]].y;
        parents[dead_parents[j]].x = children[sorted_children[i]].x;
        j++;
    }
}

prog2.c

In prog2.c, your program should contain a main function that calls the functions in ga.c, so that a population of parents is created, and children are created and added to the population for a number of generations.  A description of the main function is provided with the following psuedocode:

    start MPI     obtain the number of generations, population size, number of children, bounds for the problem, and function to evaluate from the command line
    declare variables including arrays for the parents and children
    create parents

    while i < number of generations
        create a new set of children
        add the children to the population
        increment i
    end while

    print out the individuals in the parents array
    Send parents to process 0 and print out the best of the parents
    End MPI

It should be obvious as to where each function call should be placed.  Note that in the example below, the size of the array of children should be 10 and the size of the array of parents should be 50.

Example:

With the following input, where y = x² is your expression, the output in your program may appear as follows:

Input:

numGenerations numParents numChildren startX endX functionNumber
1000 50 10 -5.0 5.0 1

Output:

Parent 0, x = 0.001, y = 0.000
Parent 1, x = 0.001, y = 0.000
Parent 2, x = -0.002, y = 0.000
Parent 3, x = 0.000, y = 0.000
Parent 4, x = -0.001, y = 0.000
Parent 5, x = -0.001, y = 0.000
Parent 6, x = 0.002, y = 0.000
Parent 7, x = 0.001, y = 0.000
Parent 8, x = -0.002, y = 0.000
Parent 9, x = 0.000, y = 0.000
Parent 10, x = 0.002, y = 0.000
Parent 11, x = 0.002, y = 0.000
Parent 12, x = -0.000, y = 0.000
Parent 13, x = -0.002, y = 0.000
Parent 14, x = -0.002, y = 0.000
Parent 15, x = 0.000, y = 0.000
Parent 16, x = 0.000, y = 0.000
Parent 17, x = 0.001, y = 0.000
Parent 18, x = 0.000, y = 0.000
Parent 19, x = 0.001, y = 0.000
Parent 20, x = 0.001, y = 0.000
Parent 21, x = 0.002, y = 0.000
Parent 22, x = 0.000, y = 0.000
Parent 23, x = 0.000, y = 0.000
Parent 24, x = -0.002, y = 0.000
Parent 25, x = -0.000, y = 0.000
Parent 26, x = 0.000, y = 0.000
Parent 27, x = -0.002, y = 0.000
Parent 28, x = 0.000, y = 0.000
Parent 29, x = -0.001, y = 0.000
Parent 30, x = -0.002, y = 0.000
Parent 31, x = -0.002, y = 0.000
Parent 32, x = 0.002, y = 0.000
Parent 33, x = 0.001, y = 0.000
Parent 34, x = -0.001, y = 0.000
Parent 35, x = 0.002, y = 0.000
Parent 36, x = 0.001, y = 0.000
Parent 37, x = -0.000, y = 0.000
Parent 38, x = 0.002, y = 0.000
Parent 39, x = -0.001, y = 0.000
Parent 40, x = -0.002, y = 0.000
Parent 41, x = 0.002, y = 0.000
Parent 42, x = -0.002, y = 0.000
Parent 43, x = -0.001, y = 0.000
Parent 44, x = 0.001, y = 0.000
Parent 45, x = 0.002, y = 0.000
Parent 46, x = -0.000, y = 0.000
Parent 47, x = 0.001, y = 0.000
Parent 48, x = 0.001, y = 0.000
Parent 49, x = -0.002, y = 0.000

The best parent was:
Parent 25, x = -0.000, y = 0.000

Your program must take input at the command line exactly as shown in the example above.  Input MUST be provided in the followng format:

numGenerations numParents numChildren startX endX functionNumber

Where numGenerations (an integer) is the number of generations to iterate over, numParents (an integer) is the number of parents, numChildren (an integer) is the number of children, startX (a double) is the lower x bound, endX (a double) is the upper x bound, and functionNumber is the function to evaluate. Several functions and their id numbers will be provided soon. Note that x² has an id of 1.   Failure to take input in the order given above will result in a loss of points on this programming assignment.

Save the source code for program 2 in files named ga.h, ga.c, and prog2.c,   Do NOT give the files different names.  You will lose points if you give the file any other names than those provided above.

To compile your program, create a makefile.  You can use the Tic-Tac-Toe example on the examples webpage to help you to create a makefile.  Note any lines in your makefile that have indention MUST contain a tab character.  make will not recognize your makefile as a valid makefile unless each indention is a tab.  Name your makefile as makefile.  Then compile your program with the following command:

    make

Assuming that there are no errors in your makefile, this will compile your program using the mpicc compiler, and it will create an executable file as long as there are no compile-time errors in your code.  Assuming that there are no errors in your program, you may run your program as follows:

prog2 numGenerations numParents numChildren startX endX functionNumber

Where prog2 is the name of your executable file.

Example Functions

Provided below are five example functions that you may use within your program.

Submission

Run your program on the Stampede Supercomputer with the Mineshaft 1 function using 10,000,000 generations, a population size of 16,000, and with 1600 children created per generation.  Run this with 16, 32, and 64 cores on the Stampede Supercomputer being sure to write down your runtimes as calculated by MPI_Wtime().

Submit your three program files, your three runtimes, an sbatch file, and your makefile, and a README file describing how to compile and run your programs, and your comparison to the eCompanion dropbox for Project 2.